Einführung
|
Von großer Bedeutung für die Kompositions- und Satztechnik ist die Einteilung der Intervalle in Konsonanzen (consonantia, lat. = Zusammenklang) und Dissonanzen (dissonantia, lat. = Auseinanderklang). Grundlage dafür bildet das Auftreten der Intervalle in der Partialtonreihe, das Verhältnis der Schwingungszahlen:
|
|
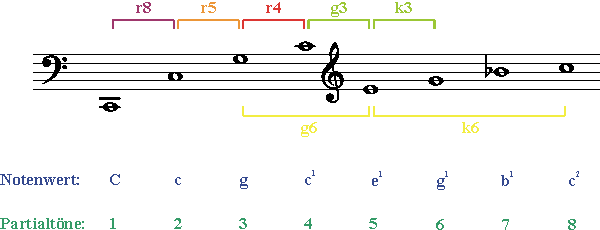
Konsonante Intervalle
|
Als konsonante Intervalle wurden zunächst nur:
-
reine Prime,
-
reine Oktave,
-
reine Quinte,
-
reine Quarte,
-
große Terz und
-
kleine Terz,
später auch noch:
-
große Sexte und
-
kleine Sexte
bezeichnet. Je kleiner das Schwingungszahlenverhältnis, desto höher derVerschmelzungsrad, am stärksten also bei den "vollkommenden" Konsonanzen Prime (1 : 1) und Oktave (1 : 2).
|
|
Dissonante Intervalle
|
Zu den dissonanten Intervallen zählen:
-
große Sekunde,
-
kleine Sekunde,
-
große Septime,
-
kleine Septime aber auch
-
die übermäßigen Intervalle und
-
die verminderten Intervalle.
Sie weisen komplizierte Schwingungszahlen verhältnisse auf.
Als Regel galt lange Zeit mehr oder weniger modifiziert, daß sich eine Dissonanz in eine Konsonanz auflösen muß, wobei diese Begriffe in jeder Musikepoche neu bestimmt wurden. Im 20. Jahrhundert verselbstständigen sich dissonantische Verbindungen zunehmend. Zu entscheiden, ob ein ein Intervall konsonant oder dissonant ist, fällt bei unseren Höhrwahrnehmungen und -gewohnheiten oft schwer. Außerdem muß beispielsweise unterschieden werden, ob eine Sekunde im melodischen Zusammenhang auftritt oder als klangliche Verschärfung eines Akkordes erscheint.
|
|
Übersicht der Konsonanten und Dissonanten Intervalle
|
|
Intervall
|
verm.
|
klein
|
rein
|
groß
|
überm.
|
|
Prime
|
|
|
0
|
|
1
|
|
Sekunde
|
|
1
|
|
2
|
3
|
|
Terz
|
2
|
3
|
|
4
|
5
|
|
Quarte
|
4
|
|
5
|
|
6
|
|
Quinte
|
6
|
|
7
|
|
8
|
|
Sexte
|
7
|
8
|
|
9
|
10
|
|
Septime
|
9
|
10
|
|
11
|
12
|
|
Oktave
|
11
|
|
12
|
|
13
|
Konsonante Intervalle
Dissonante Intervalle
|
|
